[Cub3D] DDA알고리즘을 이용한 Ray Casting

www.youtube.com/watch?v=eOCQfxRQ2pY&t=205s

lodev.org/cgtutor/raycasting.html

Raycasting

위 자료들을 참고하여 이제 실전! 코드로 옮겨보자.  

 

우선 계속 혼동이 왔던이유가 2D를 3D로 옮기는 과정에서 기준이 2D(화면 비율 그대로 연산을 함) 이어서 이걸 기준으로 3D로 옮기려고   계속 고민하다가 멘탈도 나가고 너무 하기 싫었었다.

 

위 그림은 3D로 옮기기 전 2D로 광선을 시각화 하여 구현해본 화면이다.

 

Ray Casting

레이 캐스팅의 원리를 요약해보면 시야각만큼 광선을 쏴서 그 광선이 어떤 것(벽)에 부딪히면 그 위치를 연산하여 기다란 벽을 그려주는 방식이다.  

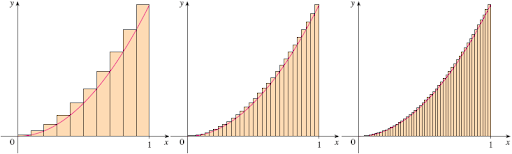
그림으로 보면 아래와 같다. 마치 구분구적법과 같은 느낌이다.

 

 

DDA알고리즘

위 그림과 같이 맵을 격자로 구분한 뒤 맵 한 칸을 선그리기에서 하나의 픽셀이라고 생각한 후 DDA알고리즘을 진행하는 방식이다.

격자의 가로축과 만나는 점(노랑), 세로축과 만나는 점(파랑)일 때, 플레이어의 위치로부터 노란점까지의 x거리와, 파란점 까지의 y거리를 구해 비교 후 짧은 쪽으로 한 스텝(맵의 한 칸을 의미) 옮겨준다.

 

같은 색부터 같은 색까지의 거리는 항상 같기 때문에 한 번 구한 다음, 다음 스탭을 위해 누적 연산을 해준다.

1번칸으로 옮긴 후 플레이어부터 두 번째 노랑점까지의 거리와 플레이어부터 첫 번째 파랑점까지의 거리를 비교하여 짧은 쪽으로 한 스탭 옮겨준다.

이를 반복하여 벽을 찾은 후 플레이어부터 벽까지의 거리를 구해준다.

 

 

코드 구현

2D를 3D로 옮기기 위해 광선의 개수는 결국 보여질 화면의 폭과 같다.

예를들면 스크린의 크기가 500 x 500이라면 총 500개의 광선이 필요하다.

따라서 아래와 같이 반복문을 구성해준다.

x = 0;
while (x < a->width)
{
   	...
    x++;
}

// 화면의 범위를 -1 ~ 1로 바꿈
a->s.screenX = 2 * x / (double)a->width - 1;
// 광선 벡터를 구하는 과정
a->s.ray = add_vector(a->p.dir, mul_vector(a->s.plane, a->s.screenX));

 

DDA알고리즘을 위해 현재 플레이어가 맵의 어디위치에 있는지를 구해준다.

// 현재 플레이어가 지도(g_map) 칸 안에 있는지 확인하기 위함
a->s.gridX = (int)(a->p.pos.x);
a->s.gridY = (int)(a->p.pos.y);

 

플레이어가 바라보고 있는 방향에 따라 스탭을 증가시켜야할지 감소시켜야할지를 정해야하기 때문에, 그 기준으로 플레이어로부터 그리드까지 거리(위 그림에서 노란점, 파란점)를 누적시켜주고, 다음 칸이 음의 방향인지 양의방향인지에 따라 -1, +1로 바꿔준다.

if (a->s.ray.x < 0)
{
	a->s.cellX = -1;
    a->s.side.x = (a->p.pos.x - a->s.gridX) * a->s.delta.x;
}
else
{
	a->s.cellX = 1;
	a->s.side.x = (a->s.gridX + 1.0f - a->p.pos.x) * a->s.delta.x;
}

if (a->s.ray.y < 0)
{
	a->s.cellY = -1;
	a->s.side.y = (a->p.pos.y - a->s.gridY) * a->s.delta.y;
}
else
{
	a->s.cellY = 1;
	a->s.side.y = (a->s.gridY + 1.0f - a->p.pos.y) * a->s.delta.y;
}

 

광선의 방향벡터를 구했다면, 비례식으로 가로축 교차점 부터 가로축 교차점 (dy), 세로축 교차점 부터 세로축 교차점(dx)까지 거리를 각각 구할 수 있다. dx, dy는 거리이므로 절대값을 이용하여 구해준다.  

a->s.delta.x = fabs(1 / a->s.ray.x);
a->s.delta.y = fabs(1 / a->s.ray.y);

 

이제 앞서 설명한 DDA과정을 이용하여 벽을 찾아내고 벽까지의 (카메라 평면과)수직거리를 구하면 된다.  

벽을 찾기위해 아래 코드를 벽을 찾을때까지 반복해준다.  

if (a->s.side.x < a->s.side.y)
{
	a->s.side.x += a->s.delta.x;
	a->s.gridX += a->s.cellX;
	a->s.isHitSide = 0;
}
else
{
	a->s.side.y += a->s.delta.y;
	a->s.gridY += a->s.cellY;
	a->s.isHitSide = 1;
}

 

카메라 평면과 수직거리는 

만약 광선이 가로축에 닿았다면, 아래 공식으로 유도할 수 있다.

a->s.distWall = (a->s.gridY - a->p.pos.y + (1 - a->s.cellY) / 2 ) / a->s.ray.y;